Exponential Distribution#

Definition#

Definition 52 (Exponential Distribution (PDF))

\(X\) is a continuous random variable with an exponential distribution if the probability density function is given by:

(19)#\[\begin{split} \pdf(x) = \begin{cases} \lambda e^{-\lambda x} & \text{if } x \geq 0 \\ 0 & \text{otherwise} \end{cases} \end{split}\]

where \(\lambda > 0\) is the rate parameter (rate of decay).

Some conventions:

  1. We write \(X \sim \exponential(\lambda)\) to indicate that \(X\) has an exponential distribution with rate parameter \(\lambda\).

Remark 4 (Exponential Distribution (PDF))

When \(\lambda = 0\), we have,

\[ \pdf(x) = \pdf(0) = \lambda e^{-\lambda 0} = \lambda e^0 = \lambda \]

This means that \(\pdf(0)\) will be more than 1 if \(\lambda > 0\) [Chan, 2021].

Definition 53 (Exponential Distribution (CDF))

If \(X\) is a continuous random variable with an exponential distribution with rate parameter \(\lambda\), then the CDF is given by integrating the PDF defined in Definition 52:

(20)#\[\begin{split} \cdf(x) = \begin{cases} 0 & \text{if } x < 0 \\ 1 - e^{-\lambda x} & \text{if } x \geq 0 \end{cases} \end{split}\]

The PDF and CDF of two exponential distributions are shown below.

 1import sys
 2from pathlib import Path
 3parent_dir = str(Path().resolve().parent)
 4sys.path.append(parent_dir)
 5
 6import numpy as np
 7import scipy.stats as stats
 8
 9from utils import seed_all, plot_continuous_pdf_and_cdf
10seed_all()
11
12# x = np.linspace(0, 10, 5000)
13lambda_1, lambda_2 = 0.5, 2
14scale_1, scale_2 = 1 / lambda_1, 1 / lambda_2
15X1 = stats.expon(scale=scale_1)
16X2 = stats.expon(scale=scale_2)
17
18plot_continuous_pdf_and_cdf(X1, 0, 10, title="Exponential$(\lambda = 0.5)$")
19plot_continuous_pdf_and_cdf(X2, 0, 10, title="Exponential$(\lambda = 2)$")

Using Seed Number 1992
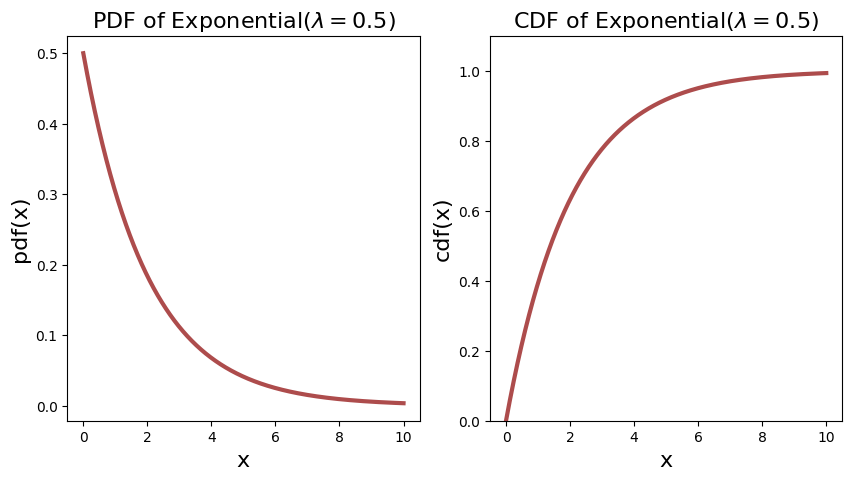
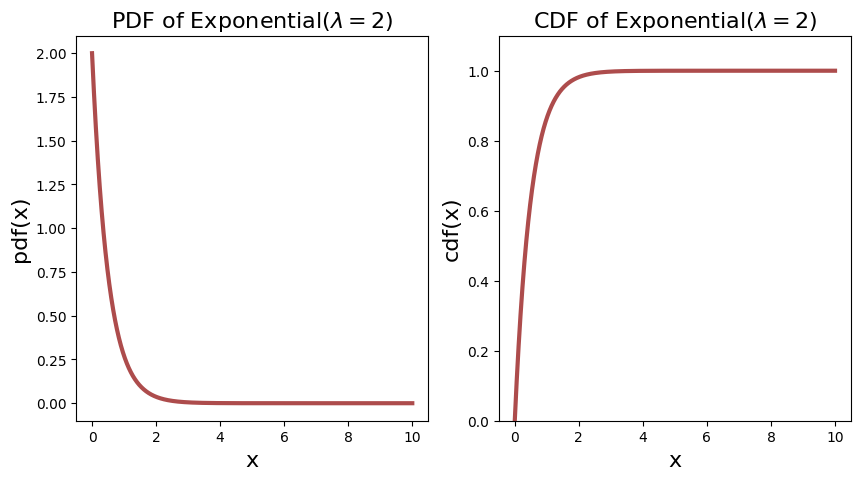
../_images/c7312d249d36b67bc5d0d9a69a6651a3520a72f7db180f3f81aa04725424ba67.png ../_images/ccf376deaa410a5b5b703eb0e15c81df21200e515affea156650d0d904dd05ec.png

Expectation and Variance#

Theorem 14 (Expectation and Variance of Exponential Distribution)

If \(X\) is a continuous random variable with an exponential distribution with rate parameter \(\lambda\), then the expectation and variance are given by:

(21)#\[ \expectation \lsq X \rsq = \frac{1}{\lambda} \qquad \text{and} \qquad \var \lsq X \rsq = \frac{1}{\lambda^2} \]

Further Readings#

Further readings is a must since Professor Chan give many intuition on how Exponential distribution is used in real life. He also showed how Exponential distribution is derived from the Poisson distribution.

  • Chan, Stanley H. “Chapter 4.5. Uniform and Exponential Random Variables.” In Introduction to Probability for Data Science, 205-211. Ann Arbor, Michigan: Michigan Publishing Services, 2021.

  • Pishro-Nik, Hossein. “Chapter 4.2.2. Exponential Distribution” In Introduction to Probability, Statistics, and Random Processes, 249-252. Kappa Research, 2014.