Conditional Probability
Contents
Conditional Probability#
Definition#
Definition 9 (Conditional Probability)
Let \(\P\) be a probability function defined over the probability space \(\pspace\).
Let \(A, B \in \E\) be events. Then the conditional probability of \(A\) given that event \(B\) has occurred is denoted
and is defined by
Intuition (Conditional Probability)#
The intuition of the conditional probability might not be immediate for beginners.
The answer here illustrate the intuition. We will quote it here:
Informally, Fig. 3 gives you an idea: the shaded area belong to both \(A\) and \(B\), So given \(B\) has happened, what then, is the probability of event \(A\) occurring? In particular, in the sample space \(B\) now, there is only a portion of \(A\) there, and one sees that portion is \(P(A \cap B) = P(A)\).
A good intuition is given that \(B\) occurred—with or without \(A\)—what is the probability of \(A\)? I.e, we are now in the universe in which \(B\) occurred - which is the full right circle. In that circle, the probability of A is the area of A intersect B divided by the area of the circle - or in other words, the number of outcomes of \(A\) in the right circle (which is \(n(A \cap B)\), over the number of outcomes of the reduced sample space \(B\).
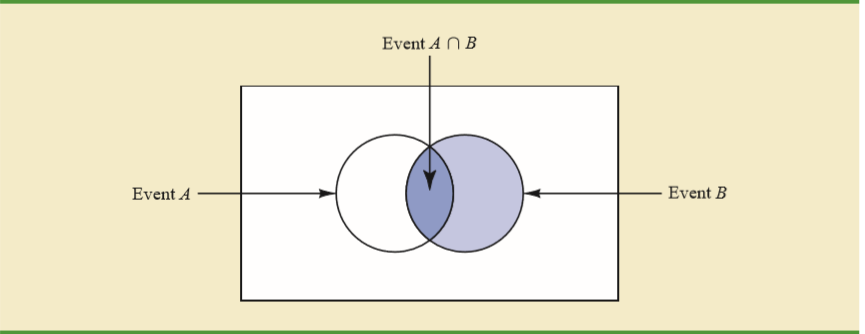
Fig. 3 Figure 1: Conditional Probability#
Therefore, after the intuition, one should not be constantly checking what the formula represents, if we have \(\P(A ~|~ B)\), then it just means given \(B\) has happened, what is the probability of \(A\) happening? The logic becomes apparent when we reduce the whole sample space \(\S\) to be only \(B\) now, and that whatever \(A\) overlaps with \(B\) will be the probability of this conditional.
Propositions#
Proposition 1 (Conditional Probability Equalities)
a) If \(\P(A) < \P(B)\), then \(\P(A|B) < \P(B|A)\)
b) If \(\P(A) > \P(B)\), then \(\P(A|B) > \P(B|A)\)
c) If \(\P(A) = \P(B)\), then \(\P(A|B) = \P(B|A)\)
