The Importance of Feature Scaling in KNN

import math
import os
import sys  # noqa

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn import datasets, neighbors
from sklearn.datasets import load_iris
from sklearn.metrics import *
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler, normalize
import sys
from pathlib import Path

Deprecated (To review before deleting)

Read this post

We need to normalize our data before performing KNN. The reasons are as follows, and for visualization see notebook’s Normalization Section.

Suppose you had a dataset (m “examples” by n “features”) and all but one feature dimension had values strictly between 0 and 1, while a single feature dimension had values that range from -1000000 to 1000000. When taking the euclidean distance between pairs of “examples”, the values of the feature dimensions that range between 0 and 1 may become uninformative and the algorithm would essentially rely on the single dimension whose values are substantially larger. Just work out some example euclidean distance calculations and you can understand how the scale affects the nearest neighbor computation.

KNN is going to be effected the most. Since KNN just looks at the euclidean distance between data points scale matters hugely. Imagine you have one set of features A with values ranging between 0 and 105 and another B with values ranging from 0 to 1. A will dominate this model because even if you have values at the maximum possible difference possible between the B values it will only be equivalent to a minuscule difference in A.

From Introduction to Statistical Learning, it is also mentioned that:

Because the KNN classifier predicts the class of a given test observation by identifying the observations that are nearest to it, the scale of the variables matters. Variables that are on a large scale will have a much larger effect on the distance between the observations, and hence on the KNN classifier, than variables that are on a small scale. For instance, imagine a data set that contains two variables, salary and age (measured in dollars and years, respectively). As far as KNN is concerned, a difference of 1,000 in salary is enormous compared to a difference of 50 years in age. Consequently, salary will drive the KNN classification results, and age will have almost no effect. This is contrary to our intuition that a salary difference of 1,000 is quite small compared to an age difference of 50 years. Furthermore, the importance of scale to the KNN classifier leads to another issue: if we measured salary in Japanese yen, or if we measured age in minutes, then we’d get quite different classification results from what we get if these two variables are measured in dollars and years.

Normalization

Normalization is a critical preprocessing step when using the K-NN algorithm. The reasons for this requirement are elaborated below, and further visualization can be found in the notebook’s Normalization Section.

Impact of Scale

Suppose a dataset consists of \(m\) examples and \(n\) features, where all but one feature dimension have values strictly between 0 and 1, while a single feature dimension has values ranging from -1000000 to 1000000. In such a scenario, the Euclidean distance between pairs of examples will be dominated by the feature with the large scale.

Scale Sensitivity of K-NN

The K-NN algorithm relies on the Euclidean distance between data points, making it highly sensitive to the scale of the features. If there’s a discrepancy in the scale across different features, the feature with the larger scale will overshadow the others, leading to biased predictions.

For instance, consider two features \(A\) with values ranging between 0 and 105, and \(B\) with values ranging from 0 to 1. The distance measure will be disproportionately affected by feature \(A\), making feature \(B\) nearly irrelevant in the classification process.

Practical Example: Salary and Age

To further illustrate the impact of scale on the K-NN algorithm, consider a dataset containing two variables: salary (measured in dollars) and age (measured in years). A difference of 1,000 in salary might appear substantial compared to a difference of 50 years in age when using the Euclidean distance. This would lead salary to dominate the K-NN classification results, rendering age almost ineffective.

However, intuitively, a salary difference of 1,000 might be considered small compared to an age difference of 50 years. Furthermore, if salary were measured in a different currency (e.g., Japanese yen) or age were measured in a different unit (e.g., minutes), the classification results would differ significantly.

Conclusion

The importance of normalization in the K-NN algorithm stems from its reliance on the Euclidean distance metric, which is highly sensitive to the scale of the features. Without normalization, features with larger scales can unduly influence the algorithm’s predictions, leading to biased and potentially inaccurate results. Therefore, normalization ensures that all features contribute equally to the distance computation, aligning the algorithm with the underlying patterns in the data.

# load wine dataset
wine = datasets.load_wine()

# purposely load it in dataframe for a better idea of our data
wine = pd.DataFrame(
    data=np.c_[wine["data"], wine["target"]], columns=wine["feature_names"] + ["target"]
)


# set X to be the df without our target y | note the same can be achieved by calling wine.data
X = wine.drop("target", axis=1)

# Take only 2 features for simplicity
X = X[["alcalinity_of_ash", "hue"]].values

# set y to be our ground truth targets
y = wine["target"].values

# train test split
X_train, X_test, y_train, y_test = train_test_split(X, y)

# call the unscaled model and fit on train
knn_unnormalized = KNeighborsClassifier(n_neighbors=1).fit(X_train, y_train)

# predict on X_test
y_test_unnormalized_preds = knn_unnormalized.predict(X_test)

# find accuracy score for unscaled model
print("KNN unscaled accuracy:", knn_unnormalized.score(X_test, y_test))

# call standard scaler which is just scaling function
ss = StandardScaler()
X_scaled = ss.fit_transform(X)
# Technically we should not scale train and test together. But for simplicity we do this and split again.
X_train_scaled, X_test_scaled, y_train, y_test = train_test_split(X_scaled, y)

# call the scaled model and fit on train
knn_normalized = KNeighborsClassifier(n_neighbors=1).fit(X_train_scaled, y_train)
y_test_normalized_preds = knn_normalized.predict(X_test_scaled)

print("KNN scaled accuracy:", knn_normalized.score(X_test_scaled, y_test))
# Find the point in which the predictions disagree for the scaled and unscaled model
# Note that we just take one diagreement to make a point in the plots later

unscaled_input, scaled_input = [], []

# find difference in between scaled vs unscaled, and also want scaled pred to be equal to ground truth for the sake of argument here
for index, (unscaled_pred, scaled_pred) in enumerate(
    zip(y_test_unnormalized_preds, y_test_normalized_preds)
):

    if unscaled_pred != scaled_pred and scaled_pred == y_test[index]:
        unscaled_input.append(X_test[index])
        scaled_input.append(X_test_scaled[index])
        print(f"index of diagreement: {index}")
        print(
            f"Unscaled inputs : {X_test[index]}\nScaled inputs : {X_test_scaled[index]}"
        )
        print(
            f"\nGround Truth : {y_test[index]}\nUnscaled prediction : {y_test_unnormalized_preds[index]}\nScaled prediction : {y_test_normalized_preds[index]}\n"
        )

        print(
            f"Nearest Neighbour of xq for unscaled : {X_train[knn_unnormalized.kneighbors([X_test[index]], return_distance=True)[1][0][0]]}"
        )
        print(
            f"Nearest Neighbour of xq for scaled : {X_train_scaled[knn_normalized.kneighbors([X_test_scaled[index]], return_distance=True)[1][0][0]]}"
        )
        print()

        print(
            f"Euclidean Distance of Nearest Neighbour of xq for unscaled : {knn_unnormalized.kneighbors([X_test[index]], return_distance=True)[0][0][0]}"
        )
        print(
            f"Euclidean Distance of Nearest Neighbour of xq for scaled : {knn_normalized.kneighbors([X_test_scaled[index]], return_distance=True)[0][0][0]}"
        )
        print()

# 2 features, call x1 alcalinity, x2 hue
alcalinity_of_ash, hue = X_train[:, 0], X_train[:, 1]
# get min and max of both features for our plot later
min_alcalinity_of_ash, max_alcalinity_of_ash = alcalinity_of_ash.min(), alcalinity_of_ash.max()
min_hue, max_hue = hue.min(), hue.max()

# Note that normalization is even more needed when the range is far apart, not so much of "the scale only"
# for eg, is range of both feature is the same, it might be "ok" to not normalize

print(f"pre-scale: range of alcalinity is {max_alcalinity_of_ash - min_alcalinity_of_ash} and for hue is {max_hue-min_hue}")


# 2 features, call x1 alcalinity, x2 hue
alcalinity_of_ash, hue = X_train_scaled[:, 0], X_train_scaled[:, 1]
# get min and max of both features for our plot later
min_alcalinity_of_ash_scaled, max_alcalinity_of_ash_scaled = alcalinity_of_ash.min(), alcalinity_of_ash.max()
min_hue_scaled, max_hue_scaled = hue.min(), hue.max()

# Note that normalization is even more needed when the range is far apart, not so much of "the scale only"
# for eg, is range of both feature is the same, it might be "ok" to not normalize

print(f"after-scale: range of alcalinity is {max_alcalinity_of_ash_scaled - min_alcalinity_of_ash_scaled} and for hue is {max_hue_scaled-min_hue_scaled}")

KNN unscaled accuracy: 0.6
KNN scaled accuracy: 0.6888888888888889
index of diagreement: 1
Unscaled inputs : [24.5   0.61]
Scaled inputs : [-0.92936518 -0.16430337]

Ground Truth : 0.0
Unscaled prediction : 2.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [24.5   0.74]
Nearest Neighbour of xq for scaled : [-1.01945068 -0.16430337]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.13
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.090085497686748

index of diagreement: 2
Unscaled inputs : [16.8   0.98]
Scaled inputs : [ 0.75223078 -2.09473241]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [16.8   1.07]
Nearest Neighbour of xq for scaled : [ 0.60208828 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.09000000000000008
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.42244238814288454

index of diagreement: 3
Unscaled inputs : [16.8   1.17]
Scaled inputs : [ 0.60208828 -1.83149208]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [16.8   1.07]
Nearest Neighbour of xq for scaled : [ 0.60208828 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.09999999999999987
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.1316201614711976

index of diagreement: 4
Unscaled inputs : [27.    0.67]
Scaled inputs : [-0.80925118  0.93253131]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [26.5   0.92]
Nearest Neighbour of xq for scaled : [-0.71916569  0.75703776]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.5590169943749475
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.19726475230920043

index of diagreement: 5
Unscaled inputs : [20.   0.8]
Scaled inputs : [-1.89027716 -0.29592353]

Ground Truth : 0.0
Unscaled prediction : 2.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [20.   0.7]
Nearest Neighbour of xq for scaled : [-1.34976417 -0.33979692]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.10000000000000009
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.5422906621596267

index of diagreement: 7
Unscaled inputs : [17.2   1.24]
Scaled inputs : [ 1.80322825 -1.52437837]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [17.2   1.23]
Nearest Neighbour of xq for scaled : [ 1.65308575 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.010000000000000009
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.23095617497409895

index of diagreement: 9
Unscaled inputs : [20.    1.23]
Scaled inputs : [-0.1486242  -1.30501144]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [20.    1.13]
Nearest Neighbour of xq for scaled : [-0.2987667  -1.34888482]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.10000000000000009
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.15642136442685656

index of diagreement: 13
Unscaled inputs : [16.8   1.28]
Scaled inputs : [-0.80925118  0.09893695]

Ground Truth : 1.0
Unscaled prediction : 0.0
Scaled prediction : 1.0

Nearest Neighbour of xq for unscaled : [16.8   1.07]
Nearest Neighbour of xq for scaled : [-0.74919419  0.2744305 ]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.20999999999999996
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.18548538668559575

index of diagreement: 15
Unscaled inputs : [18.    1.42]
Scaled inputs : [ 0.15166079 -1.61212515]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [18.    1.25]
Nearest Neighbour of xq for scaled : [ 0.15166079 -1.65599853]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.16999999999999993
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.04387338715706601

index of diagreement: 17
Unscaled inputs : [16.    1.01]
Scaled inputs : [-0.41888069  1.02027808]

Ground Truth : 1.0
Unscaled prediction : 0.0
Scaled prediction : 1.0

Nearest Neighbour of xq for unscaled : [16.    1.04]
Nearest Neighbour of xq for scaled : [-0.44890919  0.88865792]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.030000000000000027
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.13500213950765863

index of diagreement: 18
Unscaled inputs : [20.5   1.04]
Scaled inputs : [-0.80925118  0.49379744]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [20.4    0.906]
Nearest Neighbour of xq for scaled : [-0.86930818  0.66929099]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.16720047846821579
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.18548538668559575

index of diagreement: 20
Unscaled inputs : [16.8   0.86]
Scaled inputs : [ 0.90237327 -1.69987192]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [16.7   0.89]
Nearest Neighbour of xq for scaled : [ 0.60208828 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.10440306508910688
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.30028499228916283

index of diagreement: 22
Unscaled inputs : [19.6   1.12]
Scaled inputs : [-0.2687382   0.31830389]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [19.5   0.94]
Nearest Neighbour of xq for scaled : [-0.2687382   0.31830389]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.20591260281974086
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.0

index of diagreement: 24
Unscaled inputs : [19.5   1.25]
Scaled inputs : [2.70408323 0.05506357]

Ground Truth : 1.0
Unscaled prediction : 0.0
Scaled prediction : 1.0

Nearest Neighbour of xq for unscaled : [19.4   1.25]
Nearest Neighbour of xq for scaled : [ 2.70408323 -0.12042998]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.10000000000000142
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.17549354862826366

index of diagreement: 25
Unscaled inputs : [28.5   0.97]
Scaled inputs : [-1.65004916  0.23055711]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [28.5   0.93]
Nearest Neighbour of xq for scaled : [-1.46987817  0.2744305 ]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.039999999999999925
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.18543586943876497

index of diagreement: 29
Unscaled inputs : [24.    0.98]
Scaled inputs : [0.15166079 0.75703776]

Ground Truth : 0.0
Unscaled prediction : 2.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [24.    0.89]
Nearest Neighbour of xq for scaled : [0.15166079 0.71316437]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.08999999999999997
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.043873387157065125

index of diagreement: 31
Unscaled inputs : [22.5   0.78]
Scaled inputs : [-0.1486242  0.6254176]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [22.5   0.88]
Nearest Neighbour of xq for scaled : [-0.1185957   0.58154421]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.09999999999999998
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.05316563614379928

index of diagreement: 33
Unscaled inputs : [18.5   1.04]
Scaled inputs : [ 0.75223078 -1.56825176]

Ground Truth : 2.0
Unscaled prediction : 1.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [18.5   1.08]
Nearest Neighbour of xq for scaled : [ 0.60208828 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.040000000000000036
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.1996663117659809

index of diagreement: 38
Unscaled inputs : [17.5   0.75]
Scaled inputs : [-0.2987667  -1.21726466]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [17.5   0.82]
Nearest Neighbour of xq for scaled : [-0.2987667  -1.34888482]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.06999999999999995
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.13162016147119804

index of diagreement: 39
Unscaled inputs : [21.   1.1]
Scaled inputs : [-1.04947918  1.28351841]

Ground Truth : 1.0
Unscaled prediction : 0.0
Scaled prediction : 1.0

Nearest Neighbour of xq for unscaled : [21.    1.04]
Nearest Neighbour of xq for scaled : [-1.04947918  1.19577163]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.06000000000000005
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.08774677431413203

index of diagreement: 40
Unscaled inputs : [18.    1.16]
Scaled inputs : [ 0.60208828 -1.78761869]

Ground Truth : 2.0
Unscaled prediction : 1.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [18.    1.15]
Nearest Neighbour of xq for scaled : [ 0.60208828 -1.69987192]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.010000000000000009
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.08774677431413158

index of diagreement: 41
Unscaled inputs : [19.5   0.81]
Scaled inputs : [-0.95939368 -0.0765566 ]

Ground Truth : 0.0
Unscaled prediction : 1.0
Scaled prediction : 0.0

Nearest Neighbour of xq for unscaled : [19.5   0.75]
Nearest Neighbour of xq for scaled : [-0.98942218 -0.03268321]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.06000000000000005
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.0531656361437993

index of diagreement: 44
Unscaled inputs : [16.4   0.92]
Scaled inputs : [ 0.90237327 -0.77853079]

Ground Truth : 2.0
Unscaled prediction : 0.0
Scaled prediction : 2.0

Nearest Neighbour of xq for unscaled : [16.3   0.94]
Nearest Neighbour of xq for scaled : [ 0.60208828 -0.77853079]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.10198039027185359
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.30028499228916283

pre-scale: range of alcalinity is 18.8 and for hue is 1.23
after-scale: range of alcalinity is 5.82552885040976 and for hue is 3.9047314569788734

We take a point 26 in the prediction set as our query point x_q where the unscaled value is [10.6, 1.05] while after scaling it is [0.63211678 0.18668373]. Notice that the ground truth of this point 26 is class 1, but unscaled predicted it as class 0 but scaled predicted it correctly.

To dig further, and for simplicity sake, we are only considering one neighbour here, we return the closest point for both predictions and see that the closest point in train set to our query is as such:

range of alcalinity before scale = 18.8
range of hue before scale= 1.15

range of alcalinity after scale = 5.8
range of hue after scale= 4.25

x_q = [15.6, 1.04]

index of diagreement in test set: 6
Unscaled inputs : [15.6   1.04]
Scaled inputs : [0.75223078 0.40605066]

Ground Truth of x_q: 1.0
Unscaled prediction of x_q : 0.0
Scaled prediction of x_q: 1.0

Nearest Neighbour of xq for unscaled : [15.5   1.09]
Nearest Neighbour of xq for scaled : [0.90237327 0.44992405]

Euclidean Distance of Nearest Neighbour of xq for unscaled : 0.11180339887498919
Euclidean Distance of Nearest Neighbour of xq for scaled : 0.1564213644268565

More importantly, if you think of it, hue’s 1.04 and 1.09 has a pertubation of around 0.05/1.15 = 4.3%, while alcalinity 15.6 and 15.5 has a deviation of around 0.1/18.8 = 0.53%. Intuitively, since feature hue has a higher deviation, we would expect it to have a higher impact on deciding the final class, but if you work out the math, 0.05 squared and 0.1 squared we take higher weightage on the change in the alcalinity instead.

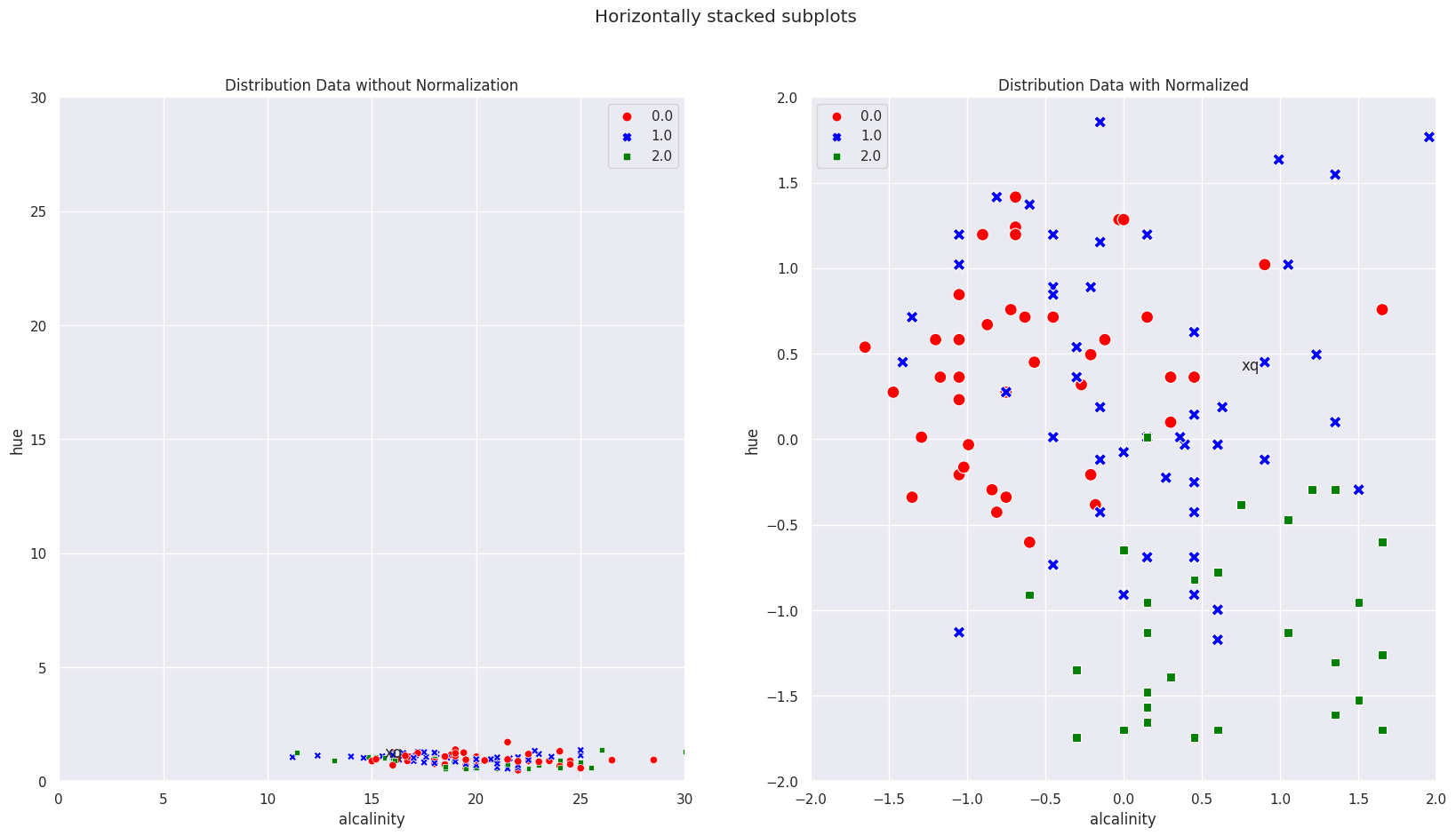
In the diagram below, (zoom out the matplotlib image), we can see geometrically how the query point is and note that it is obvious that the scaled KNN predicted it correctly.

After scaling, the range is more comparable and you can recalculate what I did in the same way as above.

Note for our drawing to be to “scale”, I purposely set the x and y axis range to be the max of the “dominating” feature, in which case its alcalinity_of_ash. So visually, we can clearly see that the range is dominated by this feature.

sns.set(rc={"figure.figsize": (20, 10)})
sns.color_palette("tab10")

fig, (ax1, ax2) = plt.subplots(1, 2)
fig.suptitle("Horizontally stacked subplots")

sns.scatterplot(x=X_train[:, 0], y=X_train[:, 1], hue=y_train, ax=ax1, palette=['red', 'blue', 'green'], style=y_train)
ax1.annotate("xq", [15.6  , 1.04])

ax1.set_xlim(0, max_alcalinity_of_ash)
ax1.set_ylim(0, max_alcalinity_of_ash)
ax1.set_title("Distribution Data without Normalization")
ax1.set(xlabel="alcalinity", ylabel="hue")




sns.scatterplot(x=X_train_scaled[:, 0], y=X_train_scaled[:, 1], hue=y_train, s=100, ax=ax2, palette=['red', 'blue', 'green'], style=y_train)
ax2.annotate("xq",  [0.75223078 ,0.40605066])
ax2.set_xlim(-2, 2)
ax2.set_ylim(-2, 2)
ax2.set_title("Distribution Data with Normalized")
ax2.set(xlabel="alcalinity", ylabel="hue")

plt.show()